2-1 ลอจิกเกต

 เกตต่าง ๆ ซ่ึงเป็ นหลักการเบ้ืองต ้ นที่เป็ นพ้ืนฐานของวงจรลอจิกน้ัน แบ่งได ้ ตาม คุณสมบตัิการทา งานไดด ้ งัน้ี
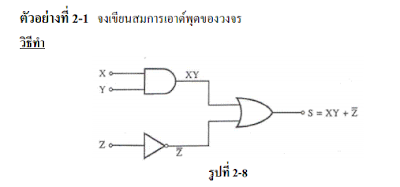
1. เกต แอนด์ (AND gate)
2. เกต ออร์ (OR gate)
3. เกต แนนด์ (NAND gate)
4. เกต นอร์ (NOR gate)
5. เกต นอต (NOT gate)
6. เกตพิเศษอื่น ๆ เช่น เกต เอกซ์คลูซิฟออร์ (Exclusive – OR gate) และเกตเอกซ์- คลูซีฟนอร์ (Exclusive-NOR gate)
    เกตต่าง ๆ เหล่าน้ีจะมีคุณสมบตัิสัญลกั ษณ ์ และวงจรที่แตกต่างกนั บางเกตจะมีขา อินพุตมากกว่า 2 ข้วั เช่น เกตแอนด์ เกตออร์ เกตแนนด์ และเกตนอร์ บางเกตอาจมีเพียง อินพุตเดียวเช่น เกตนอต หรือเกตอินเวอร ์ เตอร ์ ท้งัน้ียอ่ มข้ีนอยกู่ บัความเหมาะสม และหน้าที่ การนา ไปใชง ้ าน ส่วนขาเอาต์พุตปกติจะมีเพียงขาเดียว
2-1-1 เกต แอนด์ เกต แอนด์ สามารถท าความเข้าใจไดง ้่ายถา ้ หาก เขียนแทนด้วยสวิตช์และหลอดไฟ ซึ่ งประกอบด้วย สวิตช์ 2 ตัว คือ A และB ต่อแบบอนุกรมกนั ส่วน หลอดไฟใช้แทนเอาต์พุต Y โดยกา หนดสถานะของลอจิกดงัน้ี
             สวิตช์ปิ ด (ครบวงจร) เป็ น 1 หรือ H (High) 
            สวิตช์เปิ ด (ไม่ครบวงจร) เป็ น 0 หรือ L (Low) ห
            ลอดไฟติดสว่าง เป็ น 1 หรือ H (High) 
            หลอดไฟดับ เป็ น 0 หรือ L (Low)

จากตารางความจริงจะเห ็ นว่าในกรณี2 อินพุต เขียนสถานะของอินพุตที่ไม่ซ้า กนั ได ้ เพียง4แบบ มีเพียงสถานะเดียวเท่าน้นั ที่หลอดติดสว่างคือลา ดบั ที่4 ตารางที่เขียนข้ึนน้ีจะ เป็ นจริงเสมอและยังแสดงคุณสมบัติเฉพาะตัวของเกต แอนด์ และถ้าเขียนเป็ นสมการพีชคณิต ลอจิกของเกต แอนด์ คือ 

Y = A · B

2-1-2 เกต ออร์ เกต ออร์เขียนแทนด้วยสวิตช์และหลอดไฟ โดยให้ สวิตช์ A และ B ขนานกนั ซ่ึงเปรียบเหมือนอินพุตของ วงจร และหลอด Y เป็ นเอาต ์ พุตของวงจร โดยกา หนด สถานะลอจิกทางดา ้ นอินพุตเหมือนกบั เกต แอนด

ในตารางความจริงของเกต ออร ์ น้นั พิจารณาการทา งานในล าดับที่ 1 สวิตช์ A และ B ท้งัคู่เปิดพร ้ อมกนั หลอด Y จะดับ ได้สถานะลอจิกเป็ น “0” แต่ถา ้ หากขณะใด A หรือ B หรือ ท้งัคู่ปิด หลอด Y จะสวา่ งทนั ทีดงัน้นั เกต ออร์จึงมีสถานะเดียวที่หลอดดับหรือสถานะลอจิก เป็ น “0” เกต ออร์มีสมการพีชคณิตลอจิก คือ 

Y = A + B

2-1-3 เกตนอต เกตนอต หรื อ เกตอินเวอร์เตอร์ (Inverter gate) เขียนแทนด้วยวงจรรี เลย์ ซึ่ ง ประกอบด้วย สวิตช์ A รีเลย์ D และหลอดไฟ Y โดยกา หนดสถานะลอจิกเหมือกบั เกต แอนด์ หรือเกต ออร

จากตารางความจริง ล าดับที่ 1 ถ้าอินพุตมีสถานะ ลอจิกเป็ น “0” เอาต์พุตจะเป็ น “1” หมายถึง ถ้าสวิตช์ A เปิด หลอดไฟจะติดสว่างตลอดเวลา วงจรของรีเลยจ ์ ะไม่ ครบวงจร ท าให้คอนแท็กของรีเลย์ D ยงัคงปิดอยู่แต่ถา ้ หากขณะใดสวิตช์ A ปิ ดรีเลย์ท างาน คอนแท็กของรีเลย์จะ เปิ ดออก หลอดจะดับ ได้สถานะลอจิกเอาต์พุตเป็ น “0” สมการพีชคณิตของวงจร คือ 

 Y = A

2.4.1 เกต แนนด์ เกต แนนดเ ์ ขียนวงจรโดยการใชว ้ งจรสวิตช ์ และรีเลยป์ ระกอบกนั ดว ้ ยวงจรเกต แอนด์ และเกตอินเวอร์เตอร์(เกต แนนด์ คือ เกต น็อต-แอนด์)โดยกา หนดใหส้ วิตช์ A และ B เป็ น อินพุตของวงจร และหลอด Y เป็ นเอาตพ ์ ุตของวงจรการกา หนดสถานะของลอจิกอินพุต เหมือนกบั เกต แอนด์หรือเกต ออร

จากตารางความจริง ล าดับที่ 1 สวิตช์ A และ B เปิ ดออก รีเลย์ D ไม่ทา งาน หลอด Y จะติดสว่าง ได้ ลอจิกเป็ น “1” ล าดับที่ 2 และ 3 สวิตช์อันใดอันหนึ่ง ปิดหรือเปิด ผลที่ไดเ ้ หมือนกบัลา ดบั ที่1คือรีเลยไ์ ม่ ท างานหลอดไฟก ็ สว่างอย่สู ถานะยงัคงเป็ น “1” แต่ ในล าดับที่ 4 ท้งัสวิตช ์ A และ B ปิด สถานะลอจิกอินพุตท้งัคู่เป็ น “1” รีเลย์ท างาน ท าให้ หน้าสัมผัสของรีเลย์แบบปกติปิ ดท างาน เปิ ดออกตัดวงจร หลอดไฟ Y กจ ็ ะดบั สถานะลอจิก ขณะน้ีเป็ น “0” ส่วนสมการพีชคณิตลอจิกของวงน้ีคือ 

Y = A.B

2-1-5 เกต นอร์ เกต นอร์เขียนแทนด้วยสวิตช์ A และ B รีเลย์ D และหลอดไฟ Y ซึ่งท าหน้าที่เป็ น เอาต์พุตของวงจร(เกต นอร์คือ เกต น็อต-ออร์)

จากตารางความจริง ล าดับที่ 1 ถ้า เปิ ดสวิตช์ A และ B ไวพ ้ ร ้ อม ๆ กนั รีเลย์ D จะไม่ทา งาน หลอดไฟ Y ติด สว่าง จะได ้สถานะของลอจิกเป็ น “1” แต่ถา ้ หากขณะใดสวิตช ์ A หรือ B หรือ ท้งัคู่ปิด หลอดไฟ Y จะดับ ได้สถานะลอจิกเป็ น “0” เสมอ ส่วนสมการพีชคณิตลอจิกคือ 

Y = A + B

2.1.6 เกต เอกซ ์ คลูซีฟออร ์ เกตชนิดน้ีเกิดจากการนา เอาเกตนอต เกตแอนด ์ และเกตออร ์ มาต่อร่วมกนั สัญญาณ เอาต์พุตจะปรากฏเป็ นลอจิก “1” กต ็่อเมื่ออินพุต A และ B มีค่าเป็ นลอจิก“0” และ “1” หรือ ตรงขา ้ มกนั ถา ้ นอกเหนือจากกรณีเหล่าน้ีเอาตพ ์ ุตตะปรากฏเป็ นลอจิก“0” 

2-1.7 เกต เอกซ ์ คลูซีฟนอร ์ เกตชนิดน้ีคลา ้ ยกบั เอกซ ์ คลูซีฟ-ออร ์ เกต ซ่ึงเกิดจาก การนา เอาเกตชนิดอื่นมาประยุกต ์ใช ้ งาน แต่จะต่างกัน ตรงที่ค่าที่ไดจ ้ ากเอาตพ ์ ุตจะตรงขา ้ มกนั ถา ้สัญญาณอินพุต เป็ น “1” หรือ “0” ท้งัคู่จะเป็ นผลทา ให ้ เอาต ์ พุตเป็ น “1” ทนั ทีดงัน้นั เกตชนิดน้ีจึงเรียกอีกอยา่ งหน่ึงวา่ คอมพาราเตอร์ (Comparator)

2-2 การเขียนสมการพีชคณิตจากวงจรลอจิก

การเขียนสมการพีชคณิตจากวงจรลอจิก ใช้หลักการพิจารณาจากรูปวงจรลอจิกทีละ ส่วน เริ่มจากทางอินพุตค่อย ๆ พิจารณาไปทางเอาตพ ์ ุตเป็ นลา ดบั แลว ้ นา สมการในแต่ละเกต มารวมกนั ตามคุณสมบตัิของเกตน้ัน ๆ ชื่อของตัวแปรอินพุตและเอาต์พุต นิยมใช้ เป็ น ตวัอกัษรภาษาองักฤษ เช่น A B C D หรือ X Y Z เป็ นต้น

2-3 การเขียนวงจรลอจิกจากสมการพีชคณิต

การเขียนวงจรลอจิกจากสมการพีชคณิ ต จะต ้ องพิจารณาจากสมการเป็ นส่วน ๆ เขียนจาก ส่วนยอ่ ยไปหาส่วนใหญ่ ดงัตวัอยา่ งต่อไปน้ี
ตัวอย่างที่ 2-5 จงเขียนวงจรลอจิกจากสมการพีชคณิตต่อไป

2-4 การหาสถานะเอาต ์ พุตของวงจรลอจกิ

 การหาสถานะเอาต์พุต ของวงจรลอจิก สามารถหาได้จากการเขียนตารางความจริง (Truth table) ตารางความจริงน้ีมีหลกัการเขียนสถานะของอินพุตที่ไม่ซ้า กนั ไดโ้ ดยง่ายอาศยั เลขฐานสอง โดยกา หนดสถานะอินพุตเพียง 2 สถานะ คือ “0” หรือ “1” ตารางความจริงจะมี จา นวนกี่ช่องหรือกี่ลา ดบั น้นั ข้ึนอย่กู บัจา นวนอินพุตของวงจร เช่น 2 อินพุต ก ็ จะได ้2 2 ช่อง ดงัน้นั ถา ้ nอินพุต กจ ็ ะไดส้ ถานะของอินพุตที่ไม่ซ้า กนั เท่ากบั 2 n